Oszillator

ANALOGES FLIRT

Allgemeines

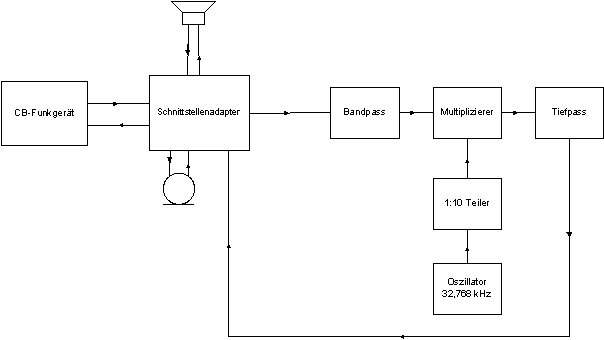
Der Oszillator wird für die Modulation benötigt.

Da wir eine Bandbreite von 300 Hz bis 3 kHz bei unserer Übertragungsstrecke haben und eine Frequenzspiegelung durchgeführt werden soll, brauchen wir einen Oszillator, der eine Modulation so vornimmt, dass 300 Hz zu 3 kHz werden und 3kHz zu 300 Hz.

Der Oszillator sollte möglichst genau und frequenzstabil sein.

Damit diese Voraussetzungen erfüllt sind, entschied ich mich für einen Quarzoszillator.

Schwingfrequenz des Quarzes

Wie schon erwähnt, soll 300 Hz zu 3,3 kHz werden.

Hier eine kurze graphische Veranschaulichung:

Ursprungssignal

Kodiertes Signal

Laut diesen Angaben ist es möglich eine Oszillatorfrequenz zu finden, die eine Modulation erzeugt und in der das untere Seitenband genau auf 300 Hz bis 3 kHz liegt.

Da wir zur Modulation einen Multiplizierer verwenden und wir das Eingangssignal mittels Kosinus ansetzen, bekommen wir eine Berechnung wie folgt:

Da wir nur das untere Seitenband benötigen, wird das obere Seitenband weggefiltert.

Nun erhalten wir nur noch den Term:

Mit diesem Term können wir nun weiterrechnen.

Wir nehmen nun an, das f = 3 kHz ist.

Wir wissen nun, dass als Resultat 300 Hz herauskommen sollten.

Somit können wir die Oszillatorfrequenz berechnen:

Somit ergibt sich eine Oszillatorfrequenz von 3.3 kHz.

Blockschaltbild

y

x

Schwingvoraussetzung

Verstärker wird bei der nachstehenden Berechnung als k bezeichnet und das Rückkoppelnetzwerk als a. k und a, wie auch y und x, sind komplexe Zahlen.

Aus dieser Berechnung folgt, dass die Verstärkung mindestens so groß wie die Abschwächung des Rückkoppelnetzwerkes sein muss.

Der Verstärker

Der Verstärker ist in unserer Schaltung mittels FET – Verstärker realisiert.

Als Verstärkertyp haben wir uns für einen BF245A entschieden.
Nachstehend einige technische Daten:

Berechnung des R_D

Annahme: IDSS = 4 mA

U1 ist die Hälfte der Versorgungsspannung -> 6 V

Daraus ergibt sich:

Nächster Widerstandswert der E24 Reihe ist 1.2 kΩ.

Daraus ergibt sich ein Spannungsabfall an R_D von:

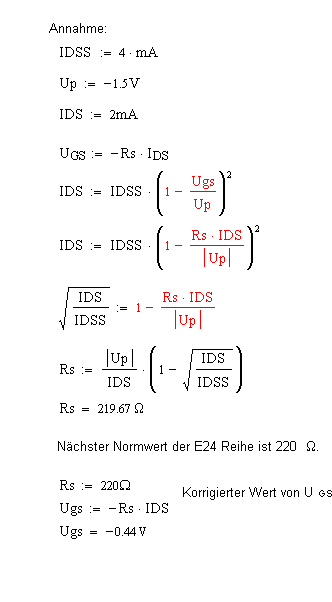
Berechnung der Verstärkung des FET – Verstärkers

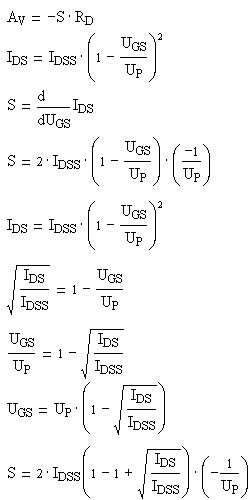
Da wir UP = -1.5V, I_DS = 2 mA und I_DSS = 4 mA gegeben haben, können wir nun die Verstärkung berechnen.

Die Verstärkung lautet dann:

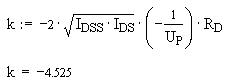
Das Rückkoppelnetzwerk

Das Rückkoppelnetzwerk besteht aus einem Quarz mit 32.768 kHz und zwei Kondensatoren, die auf Masse geschaltet sind.

Der Quarz wird in Serienresonanz betrieben. Laut einer Messung beträgt der Serienwiderstand 15 k. Laut Datenblatt hat der Serienkondensator 0.0035 pF und die Serieninduktivität 6740 H.

Schaltbild des Rückkoppelnetzwerks

Berechnung der Resonanzfrequenz des Rückkoppelnetzwerkes

Berechnung der Abschwächung des Rückkoppelnetzwerkes bei f = 33 kHz

Mit diesen zwei Formeln kann man nun die Bauteile berechnen. Die Berechnung lautet wie folgt:

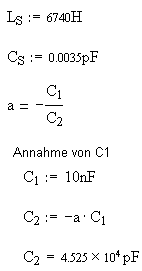
Aus dieser Gleichung ist ersichtlich, dass die Schwingbedingung erfüllt wäre, jedoch muss die Verstärkung des Verstärkers grösser als die Abschwächung des Rückkoppelnetzwerkes sein.

Da wir hier einen Quarz benutzen und dessen Güte sehr hoch ist, wird die Berechnung der Bauteile sehr komplex. Damit man diese Rechnung nicht lösen muss, werden mathematische Hilfsmittel verwendet.

Ich verwende hierfür PSpice in der Transient - Analyse.

Da PSpice die gesamte Schaltung nicht lösen kann, da der Quarz eine zu hohe Güte besitzt, berechnen wir die Schleifenverstärkung mit der AC - Analyse.

Die Kondensatoren werden wieder gleich angenommen, wie oben definiert.

Reale Berechnung des Quarzoszillators

Zur Berechnung des Quarzoszillators wird folgende Schaltung verwendet:

Nun können wir die Schaltung simulieren. Aus der Simulation interessiert uns im wesentlichen der Wert der Amplitude, bei dem die Phase 0 ist.

Die Schwingbedingung ist dann erfüllt, wenn die Verstärkung größer 1 (0 dB) ist.

Anhand des Graphen auf der nächsten Seite ist erkennbar, dass die Schwingbedingung mit den ausgewählten Werten für die Kondensatoren C₁ und C₂, erfüllt wird.

Grafische Darstellung der Übertragungsfunktion

Zur graphischen Darstellung der Übertragungsfunktion habe ich ein kurzes Programm in MATLAB 6 geschrieben.

Code des Programms

Sandholzer Markus

Graphische Darstellung der Übertragungsfunktion

Auszug aus dem Befehlsfenster in MATLAB